Implementation of an Accelerated Projected Gradient Descent Solver for Multibody Dynamics Simulation

Abstract

中文摘要

大规模多刚体非光滑动力学中的接触与摩擦求解常被表述为变分不等式或互补问题。传统的 Dantzig 与 PGS 方法在强不良条件数与高接触密度场景下容易出现收敛慢与内存压力大的问题。本文实现了一种面向多刚体仿真的加速投影梯度下降求解器，并完成与现有求解管线的集成。方法上，采用算子化的 Schur 补乘法以避免显式装配，结合 Nesterov 加速的动量策略与基于 Armijo 的回溯搜索以保证目标值单调下降，并通过盒约束裁剪与库仑摩擦圆锥投影维护可行性，同时提供跨时间步的 warm start。工程实现方面，对算子乘法与投影步骤进行数据并行化：对 J 乘与质量逆乘按“约束分块/刚体分块”进行并行划分，使用 OpenMP 实现线程级并行与线程本地工作区以避免写入冲突；对法向与切向投影进行成组批处理以降低分支与访存开销。基于上万级接触的基准测试显示，本文方法在保持物理一致性的前提下，相较 Dantzig 与 PGS 展现更稳定的收敛与更少的迭代次数；结合 warm start 与上述并行化后，实现约 1.3 至 1.6 倍的端到端加速，并因避免显式矩阵装配而降低峰值内存占用。结果表明，一阶加速与算子化并行实现对大规模非光滑动力学仿真具有良好的通用性与可扩展性。

关键词：非光滑动力学；互补问题；加速投影梯度；Armijo 回溯；摩擦圆锥；Schur 算子；算子化实现；并行计算；OpenMP；matrix free。

English Abstract

Contact and friction in large-scale non-smooth multibody dynamics are often posed as variational inequalities or complementarity problems. Classical Dantzig and PGS solvers may suffer from slow convergence and memory pressure under ill-conditioned and densely contacting scenarios. We implement an Accelerated Projected Gradient Descent solver for multibody simulation and integrate it into an existing Lagrange-multiplier pipeline. The method performs matrix-free Schur complement multiplications to avoid explicit assembly, couples Nesterov-style momentum with Armijo backtracking for monotonic decrease, and enforces feasibility via box constraints and Coulomb friction-cone projection, with warm start across time steps. On the engineering side, we parallelize both operator application and projection: J times and mass-inverse times are block-partitioned by constraints and by bodies, executed with OpenMP threads and thread-local workspaces to avoid write conflicts; normal and tangential projections are processed in batches to reduce branching and memory traffic. On benchmarks with tens of thousands of contacts, the proposed approach achieves more stable convergence and fewer iterations than Dantzig and PGS while preserving physical consistency; with warm start and parallelization, it delivers about 1.3 to 1.6× end-to-end speedup and reduces peak memory by avoiding explicit matrix assembly. These results indicate that first-order acceleration and matrix-free parallel implementation are effective and scalable for large-scale non-smooth dynamics simulation.

Keywords: non-smooth dynamics; complementarity; accelerated projected gradient; Armijo backtracking; friction cone; Schur operator; matrix-free; parallel computing; OpenMP.

Accelerated Projected Gradient Descent (APGD) 算法

1 算法背景

在非光滑动力学（Non-Smooth Dynamics）仿真中，刚体系统往往包含大量的不等式约束，如摩擦接触、单侧约束及驱动电机约束等。这些约束问题通常可转化为线性互补问题（Linear Complementarity Problem, LCP）或变分不等式问题（Variational Inequality, VI）。传统直接求解方法（如Dantzig算法）虽然精确，但在大规模问题中计算代价高且扩展性差。

投影梯度法（Projected Gradient Method, PGM）是一种广受关注的替代方案，但其收敛速度较慢，难以满足实时性要求。因此，加速投影梯度下降算法（Accelerated Projected Gradient Descent, APGD）被提出，广泛应用于非光滑动力学求解。

2 数学模型

APGD算法求解如下凸优化问题：

\[\min_{\lambda \in \mathcal{K}} \quad f(\lambda) = \frac{1}{2} \lambda^T Z \lambda + \lambda^T d\]

其中，$\lambda$ 是约束力（拉格朗日乘子），$Z \in \mathbb{R}^{n \times n}$ 是对称正定矩阵（Schur complement矩阵），$d \in \mathbb{R}^{n}$ 为右端向量，集合$\mathcal{K}$ 为约束投影集合，定义了约束的上下界。

刚体动力学中矩阵 $Z$ 典型的构造方式为：

\[Z = C_q M^{-1} C_q^T + E\]

其中，$C_q$ 为约束雅可比矩阵，$M$ 为系统质量矩阵，$E$ 为约束力混合项（Constraint Force Mixing, CFM）。

3 算法流程

APGD采用Nesterov加速技巧提高收敛速度，具体迭代流程如下：

初始化：
- $\lambda^{(0)} = 0$, $y^{(0)} = \lambda^{(0)}$, $t^{(0)} = 1$
- 确定初始步长 $L$
第 $k$ 步迭代：
1. 梯度计算：
  \[\nabla f(y^{(k)}) = Z y^{(k)} + d\]
2. 梯度步长迭代及约束投影：
  \[\lambda^{(k+1)} = \Pi_{\mathcal{K}} \left(y^{(k)} - \frac{1}{L}\nabla f(y^{(k)})\right)\]
3. 更新加速参数：
  \[t^{(k+1)} = \frac{1 + \sqrt{1 + 4(t^{(k)})^2}}{2}\]
4. 估计下一迭代点：
  \[y^{(k+1)} = \lambda^{(k+1)} + \frac{t^{(k)} - 1}{t^{(k+1)}}(\lambda^{(k+1)} - \lambda^{(k)})\]

重复上述过程直至满足收敛准则。

4 约束投影操作

投影操作 $\Pi_{\mathcal{K}}(\cdot)$ 针对不同类型约束定义为：

单边约束（Unilateral）：
\[\Pi_{[0, \infty)}(x) = \max(0, x)\]
有界约束（Motor约束）：
\[\Pi_{[l, h]}(x) = \min(\max(x, l), h)\]
摩擦锥约束（Coulomb friction cone）：确保摩擦力不超过最大静摩擦力。

5 收敛性分析

APGD算法具有$O(1/k^2)$的加速收敛性，其中$k$为迭代次数。相比传统的PGM方法（$O(1/k)$），APGD显著提高了收敛速度。实践中，初始步长$L$及约束边界的选择对收敛影响显著，需合理设置。

6 参数调控策略

为确保算法稳定性和收敛性，需进行如下参数调控：

动态步长（Step Size）：使用回溯线搜索动态调整。
Warm-Start：利用前一步求解的$\lambda$作为迭代初始点。
迭代停止准则：设定误差阈值$\varepsilon$：
\[\| \lambda^{(k+1)} - \lambda^{(k)} \| \le \varepsilon\]

7 实际应用

APGD算法成功应用于大规模接触摩擦系统、机器人关节、电机驱动器约束等非光滑动力学问题。特别地，Motor约束通常设置为较大有限上下界，如$[-10^6, 10^6]$，以保证算法收敛。

8 关键优化策略

Warm Start：显著减少迭代次数。
摩擦约束处理：确保摩擦力投影满足物理约束。
自适应步长：结合Armijo条件回溯调整步长。
非单调策略：允许短暂的目标函数上升以提升鲁棒性。

9 数值表现与参数影响

实际仿真显示，APGD算法迭代次数和步长对收敛性能影响明显。过高迭代次数可能提高精度但增加计算成本甚至引发数值不稳定现象。应根据具体动力学场景选取合适参数，平衡计算性能与精度。

10 小结与展望

APGD算法通过加速策略显著提升求解效率，尤其适用于大规模并行计算。未来研究可关注参数自动调整及不同投影方法对算法性能的进一步影响。

参考文献

Anitescu, M., et al. (1997). Time-stepping for rigid body dynamics. Computer Methods in Applied Mechanics and Engineering.
Tasora, A., et al. (2015). Chrono: An Open Source Multi-physics Dynamics Engine. International Conference on High Performance Computing in Science and Engineering.
Project Chrono. Chrono Engine Documentation. http://projectchrono.org.
Serban, R. et al. (2014). ChIterativeSolverVI.cpp, Project Chrono. https://github.com/projectchrono/chrono.

伪代码

A P G D

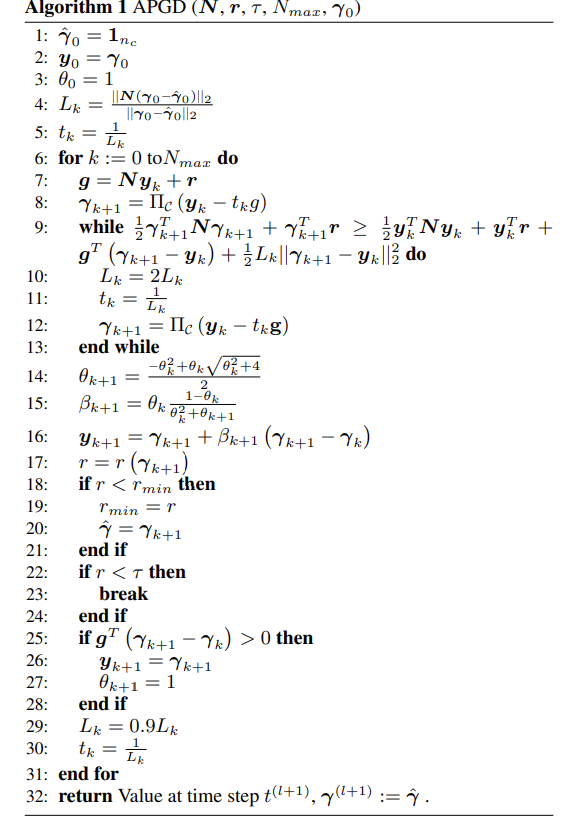
讲解：

问题与符号

我们在约束力空间中解一个带投影的二次优化：

\[\min_{\gamma\in \mathcal{C}} f(\gamma)=\tfrac12\,\gamma^\top N\,\gamma + r^\top \gamma ,\]

其中

$N$ 是Delassus 矩阵（对称半正定，来源于 $C M^{-1}C^\top$ 等），
$r$ 是右端项（由自由速度、稳定化、CFM 等组成），
$\mathcal{C}$ 是可行集：无摩擦时是正正交（$\gamma\ge0$），有摩擦时是摩擦锥的直积（逐接触块做投影）。
目标的梯度是 $\nabla f(\gamma)=N\gamma+r$。这是 APGD/FISTA 在多体接触里常用的形式（Chrono、Anitescu–Tasora、TOG 等文献都用这一范式）。(web.cels.anl.gov, air.unipr.it)

逐行讲解（完全对齐你图里的行号）

输入： $(N, r, \tau, N_{\max}, \gamma_0)$。 $\tau$ 是停止阈值（对残差/违约度），$N_{\max}$ 是最大迭代数，$\gamma_0$ 初值。

第 1 行 $\tilde{\gamma}{0} = 1{n_c}$ 取一个与 $\gamma_{0}$ 不同的向量（这里是全 1 向量），仅用于初始化 Lipschitz 常数的“割线”估计（见第 4 行）。直觉：用两点之间的斜率近似 $|N|_2$。

第 2 行 $y_0 = \gamma_0$ 动量点（外推点）初始化等于当前点。FISTA/加速 PG 都用两条轨迹：$y_k$（外推点）与 $\gamma_k$（主迭代）。(ceremade.dauphine.fr)

第 3 行 $\theta_0 = 1$ Nesterov 动量参数的初值。常见做法：$\theta_0=1$。(ceremade.dauphine.fr)

第 4 行 $L_k = ||N(\gamma_0-\tilde\gamma_0)||_2 / ||\gamma_0-\tilde\gamma_0||_2$ 对 $L\approx|N|_2$ 的初始谱界（割线估计）。真实 $L$ 不易得，先给一个估计，后续用回溯线搜修正（第 9–13 行）。这类“未知 $L$ 场景的回溯”是 FISTA/加速 PG 的标准配置。(ceremade.dauphine.fr, ww3.math.ucla.edu)

第 5 行 $t_k = 1/L_k$ 迭代步长（学习率）。注意：这是数值迭代步长，不是仿真时间步；它只控制“这一步走多远”。（这一点和我们前面讨论一致。）

第 6 行 $for k = 0..N_max do$ 主循环：同一物理时间步内，做最多 $N_{\max}$ 次 APGD 迭代。

第 7 行 $g = N y_k + r$ 在外推点 $y_k$ 计算梯度 $g=\nabla f(y_k)$。

第 8 行 $\gamma_{k+1} = \Pi_\mathcal{C}(y_k - t_k g)$ 一次投影梯度步：先沿负梯度走，再对集合 $\mathcal{C}$ 做投影。

无摩擦：$\Pi_{\mathbb{R}^+}(\cdot)=\max(0,\cdot)$ 逐分量截断；
有摩擦：每个接触块做摩擦锥投影：若 $\lambda_n\le0$ 置零；否则令 $|\lambda_t|\le\mu\lambda_n$，超出则缩回圆锥母线（常用欧氏投影）。这一步把“摩擦与非穿透”显式编码到迭代中。(web.cels.anl.gov)

第 9 行 $while … do$ 回溯线搜索（Armijo/光滑性不等式）：检查

\[f(\gamma_{k+1}) \;\le\; f(y_k)+g^\top(\gamma_{k+1}-y_k) +\tfrac12 L_k\|\gamma_{k+1}-y_k\|^2 .\]

若不成立（你图里是“$\ge$”进入 while），说明当前 $L_k$ 偏小，需要增大 $L_k$（即减小步长）。(ceremade.dauphine.fr)

第 10 行 $L_k = 2 L_k$ 把 Lipschitz 估计翻倍（保守化），常见经验做法。

第 11 行 $t_k = 1/L_k$ 随之更新步长。

第 12 行 $\gamma_{k+1} = \Pi_\mathcal{C}(y_k - t_k g)$ 用更小步长重算一次投影梯度步。

第 13 行 $end while$ 直到满足光滑性上界为止。这样即便最初 $L$ 估错，也保证稳定下降。(ceremade.dauphine.fr)

第 14 行 $\theta_{k+1} = \frac{-\theta_k^2 + \theta_k\sqrt{\theta_k^2+4}}{2}$ Nesterov 加速的参数更新（FISTA 族的一种等价写法），把一阶法收敛率从 $\mathcal{O}(1/k)$ 提升到 $\mathcal{O}(1/k^2)$（凸情形）。(ceremade.dauphine.fr)

第 15 行 $\beta_{k+1} = \frac{\theta_k(2-\theta_k)}{\theta_k^2+\theta_{k+1}}$ 动量系数 $\beta_{k+1}$ 的具体配方（与第 14 行联动）。不同论文写法等价；核心是用 $\theta$ 构造外推权重。(seas.ucla.edu)

第 16 行 $y_{k+1} = \gamma_{k+1} + \beta_{k+1}(\gamma_{k+1}-\gamma_k)$ 外推：把“最新下降方向”外推到 $y_{k+1}$。这是加速的关键。

第 17 行 $r = r(\gamma_{k+1})$ 计算当前迭代的残差/违约度（实现里可用 KKT 残差、互补度、最大违约等任一度量），用于“记录最优点”和“早停”。

第 18–21 行 如果当前 $r$ 刷新了历史最小值，就记录最佳迭代 $\hat\gamma=\gamma_{k+1}$。这是“最优点跟踪”（monotone 变体常见），避免动量带来的函数值回弹。

第 22–24 行 若 $r<\tau$ 达到精度阈值，提前停止。

第 25 行 $if g^\top(\gamma_{k+1}-\gamma_k) > 0 then$ 动量重启判据（gradient scheme）：当动量方向与梯度“拧巴”（内积为正，说明有过冲迹象），就执行重启。这正是 O’Donoghue & Candès 提出的自适应重启思想之一（函数/梯度两种等价触发），在大量问题上显著提升稳健性。(arXiv)

第 26–27 行 重启动作：$y_{k+1} = \gamma_{k+1}$, $\theta_{k+1} = 1$。把动量清零，回到“纯 PG”的状态，从而抑制振荡。(arXiv)

第 29 行 $L_k = 0.9 L_k$ 非增回溯小技巧：在下一步开始前，把 $L_k$ 轻微下调（允许更大胆的步长）。很多现代 FISTA/backtracking 论文建议让 $L_k$ 不单调地尝试变小，以减少不必要的保守性，下次若过大再由第 9–13 行自动“回溯”放大。(ww3.math.ucla.edu, arXiv)

第 30 行 $t_k = 1/L_k$ 同步更新步长备用。

第 31 行 $end for$ 主循环结束（达到 $N_{\max}$ 或中途已早停）。

第 32 行 $return … \gamma^{(\ell+1)} := \hat\gamma$ 返回当前时间步的最优解（或最佳迭代 $\hat\gamma$）。这里 $\ell$ 只是外层时间步索引的记号：外层时间步 $h$ 早已固定，本算法只是在这一帧里把 $\gamma$ 解好。

这些步骤“为什么这么设计”——直觉与联系

回溯线搜（第 9–13 行）：保障“光滑上界”成立 ⇒ 即便 $L$ 不知道，也能稳定下降。(ceremade.dauphine.fr)
Nesterov 加速（第 14–16 行）：把一阶法拉到 $\mathcal{O}(1/k^2)$ 的最佳阶；但会引入“过冲/回弹”。(ceremade.dauphine.fr)
自适应重启（第 25–28 行）：当检测到过冲（常用的“gradient scheme”判据）就清掉动量，恢复收敛。这个技巧在实践中非常重要。(arXiv)
$L$ 递减（第 29–30 行）：给下一次迭代一个更“激进”的起点；如果激进过头，回溯再把它拉回去（第 9–13 行）。(ww3.math.ucla.edu)

在摩擦锥上的投影（第 8/12 行的细节）

对每个接触 $i$ 的块 $\gamma_i=[\lambda_{n,i}; \boldsymbol{\lambda}_{t,i}]$（法向+切向）

若 $\lambda_{n,i}\le 0$：$\gamma_i\leftarrow \mathbf{0}$；
否则令 $t=|\boldsymbol{\lambda}_{t,i}|$，
- 若 $t\le \mu \lambda_{n,i}$：保持不变；
- 若 $t>\mu \lambda_{n,i}$：
  \[\boldsymbol{\lambda}_{t,i}\leftarrow \mu \lambda_{n,i}\,\frac{\boldsymbol{\lambda}_{t,i}}{t}.\]

该投影是逐块且完全可并行的，这正是 APGD 在大规模接触里高效的原因之一。(web.cels.anl.gov, 科学直达)

和多体接触文献/实现的对应

将接触问题写成 QP/VI + 块投影的思路：Anitescu–Tasora 的 CCP 框架与后续众多实现（含 Chrono）。(web.cels.anl.gov, OSTI)
用 Nesterov 加速 的 APGD 解接触：TOG 论文把 APGD 引入多体接触并给出加速收益实证。(air.unipr.it)
回溯线搜 + 自适应重启：来自 FISTA 与 O’Donoghue–Candès 的加速/重启体系，工程上非常通用、稳健。(ceremade.dauphine.fr, arXiv)
参数自由/非增回溯：近期工作进一步主张用组合的回溯与重启以减少手动调参。(ww3.math.ucla.edu)

一点实现提示（落到代码）

第 7 行 g = N*y + r——可通过“矩阵-向量乘”或“系统乘（不显式组装）”实现，以保持稀疏/分布式效率。
第 8/12 行的 $\Pi_\mathcal{C}$——把非负投影与摩擦锥投影分开写（逐块），CPU 上可 OpenMP 并行，GPU 上天然并行。
第 9–13 行回溯——用“最多 $B_{\max}$ 次回溯”防死循环；没通过时翻倍 $L$；通过后记得缓存本次 $L$（第 29 行会再下调 0.9）。
残差 r(·)——建议用“投影梯度映射范数”、互补量或最大违约，和你的 $\tau$ 标尺一致即可。
重启（第 25–28 行）——务必同时把 y_{k+1}←γ_{k+1} 和 θ_{k+1}←1 两步都做，全量清掉动量。

小结（把核心思路再压一句）

第 7–13 行：在 $y_k$ 处做投影梯度 + 回溯，保证稳定下降；
第 14–16 行：用 Nesterov 外推加速；
第 17–24 行：记录最优点 + 早停；
第 25–28 行：自适应重启抑制过冲；
第 29–30 行：下调 $L$ 让下一步更大胆，必要时再回溯。