2. NCP -> QP
在三维欧氏空间中描述刚体 $j$ 的位置与姿态的广义坐标分别为 $\mathbf{r}_j \in \mathbb{R}^3$ 与 $\boldsymbol{\varepsilon}_j \in \mathbb{R}^4$。前者给出刚体 $j$ 质心的绝对位置,后者为一组欧拉参数(四元数),用于在全局参考系下表征刚体的取向。由 $n_b$ 个刚体组成的系统,其广义坐标集合写作
\[\mathbf{q}=\begin{bmatrix} \mathbf{r}_1^{\mathsf T},\ \boldsymbol{\varepsilon}_1^{\mathsf T},\ \ldots,\ \mathbf{r}_{n_b}^{\mathsf T},\ \boldsymbol{\varepsilon}_{n_b}^{\mathsf T} \end{bmatrix}^{\mathsf T}\in\mathbb{R}^{7n_b},\]其时间导数为
\[\dot{\mathbf{q}}=\begin{bmatrix} \dot{\mathbf{r}}_1^{\mathsf T},\ \dot{\boldsymbol{\varepsilon}}_1^{\mathsf T},\ \ldots,\ \dot{\mathbf{r}}_{n_b}^{\mathsf T},\ \dot{\boldsymbol{\varepsilon}}_{n_b}^{\mathsf T} \end{bmatrix}^{\mathsf T}\in\mathbb{R}^{7n_b}.\]为了建立牛顿–欧拉方程,本文不直接使用 $\dot{\mathbf{q}}$,而改用
\[\mathbf{v}=\begin{bmatrix} \dot{\mathbf{r}}_1^{\mathsf T},\ \boldsymbol{\omega}_1^{\mathsf T},\ \ldots,\ \dot{\mathbf{r}}_{n_b}^{\mathsf T},\ \boldsymbol{\omega}_{n_b}^{\mathsf T} \end{bmatrix}^{\mathsf T}\in\mathbb{R}^{6n_b},\]其优点在于:(i)未知量更少;(ii)可得到常数、对称且正定的质量矩阵。
对每一个刚体 $B$,存在一个简单的线性变换,将其以体固系表达的角速度 $\bar{\boldsymbol{\omega}}_B$ 与欧拉参数的时间导数 $\dot{\boldsymbol{\varepsilon}}_B$ 相联系。具体为
\[\bar{\boldsymbol{\omega}}_B = 2\,\mathbf{G}\!\left(\boldsymbol{\varepsilon}_B\right)\,\dot{\boldsymbol{\varepsilon}}_B,\]其中矩阵 $\mathbf{G}\in\mathbb{R}^{3\times4}$ 的各元素线性依赖于欧拉参数 $\boldsymbol{\varepsilon}_B$。
\(\mathbf G(\boldsymbol\varepsilon)=
\begin{bmatrix}
-e_1 & e_0 & e_3 & -e_2\\
-e_2 & -e_3 & e_0 & e_1\\
-e_3 & e_2 & -e_1 & e_0
\end{bmatrix}.\)
(不同版本可能只差符号或行列顺序,本质等价。)
定义分块对角矩阵
\[\mathbf{L}(\mathbf{q}) \equiv \mathrm{diag}\!\Big[ \mathbf{I}_{3\times3},\ \tfrac{1}{2}\mathbf{G}^{\mathsf T}(\boldsymbol{\varepsilon}_1),\ \ldots,\ \mathbf{I}_{3\times3},\ \tfrac{1}{2}\mathbf{G}^{\mathsf T}(\boldsymbol{\varepsilon}_{n_b}) \Big]\in\mathbb{R}^{7n_b\times6n_b},\]其中 $\mathbf{I}_{3\times3}$ 为单位阵,则有
\[\dot{\mathbf{q}}=\mathbf{L}(\mathbf{q})\,\mathbf{v}.\]把“物理速度”转换成“参数速度”
因为建模/求解用 $\mathbf v$ 更舒服,但积分与几何都离不开 $\dot{\mathbf q}$。
所以做法是“混合坐标”:方程里用 $\mathbf v=[\dot{\mathbf r};\boldsymbol\omega]$ 去写牛顿–欧拉方程,解完后再用
\[\dot{\mathbf q}=\mathbf L(\mathbf q)\,\mathbf v\]把它变回“参数速度”,以更新位姿、计算雅可比与约束速度。
2.1 建模要点(Modeling Aspects)
考虑图 1 中所示的两刚体 $A$ 与 $B$ 的接触。对物体 $A$,在接触点 $i$ 处取法向量 $\mathbf{n}{i,A}$,其与该点的切平面正交,并指向物体 $A$ 的外部。再选取两条互相正交的单位向量 $\mathbf{u}{i,A}$ 与 $\mathbf{w}{i,A}$,与 $\mathbf{n}{i,A}$ 一起在 $A$ 上构成右手坐标系,作为接触点 $i$ 的局部参考系。对物体 $B$ 亦按同样步骤定义,以 $\mathbf{n}{i,B},\,\mathbf{u}{i,B},\,\mathbf{w}_{i,B}\in\mathbb{R}^3$ 构成其局部系。
与接触 $i$ 相关联的拉格朗日乘子 $\hat{\gamma}_i$ 被用来就间隙(距离)函数 $\Phi$ 在两物体 $A$ 与 $B$ 之间建立互补性条件:
\[0 \le \hat{\gamma}_{i,n}\ \perp\ \Phi_i(\mathbf{q}) \ge 0 .\]当两物体恰好接触时,$\Phi_i(\mathbf{q})=0$;否则 $\Phi_i(\mathbf{q})>0$。若接触几何在接触处光滑且凸,则构造 $\Phi_i(\mathbf{q})$ 相对直接。对于复杂且/或非凸的几何,精确定义 $\Phi_i(\mathbf{q})$ 可能较为困难,这超出了本文讨论范围。
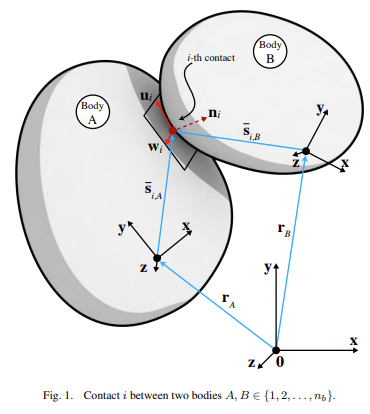
约定,$\alpha_i \equiv \alpha_i,A$,其中 $\alpha \in {\mathbf n,\mathbf u,\mathbf w}$。与接触点 $i$ 相关的接触力可分解为法向分量与切向分量。 法向分量:
\[\mathbf F_{i,N}=\hat\gamma_{i,n}\,\mathbf n_i,\]切向分量:
\[\mathbf F_{i,T}=\hat\gamma_{i,u}\,\mathbf u_i+\hat\gamma_{i,w}\,\mathbf w_i,\]其中乘子 $\hat\gamma_{i,n}\ge 0,\ \hat\gamma_{i,u},\ \hat\gamma_{i,w}$ 表示各方向上的力幅值。摩擦力假设满足库仑干摩擦模型可写为
圆锥约束(不等式)
互补条件(粘—滑切换)
方向对齐(反向做功) $$ \begin{equation} \sqrt{\hat\gamma_{i,u}^{\,2}+\hat\gamma_{i,w}^{\,2}}\le \mu_i\,\hat\gamma_{i,n}\qquad
|\mathbf v_{i,T}|! \left(\sqrt{\hat\gamma_{i,u}^{\,2}+\hat\gamma_{i,w}^{\,2}}-\mu_i\,\hat\gamma_{i,n}\right)=0,\qquad \left\langle \mathbf F_{i,T},\,\mathbf v_{i,T}\right\rangle=-|\mathbf F_{i,T}|\,|\mathbf v_{i,T}|, \end{equation} $$
其中 $\mathbf v_{i,T}$ 为在接触点处刚体 $A$ 与 $B$ 的相对切向速度。以上方程是如下优化问题的一阶 Karush–Kuhn–Tucker(KKT)最优性条件,该优化问题在两个虚变量 $y,z\in\mathbb R$ 上定义:
\[\begin{equation} \big(\hat\gamma_{i,u},\hat\gamma_{i,w}\big) =\operatorname*{arg\,min}_{\sqrt{y^{2}+z^{2}}\le \mu_i\,\hat\gamma_{i,n}} \ \mathbf v_{i,T}^{\top}\big(y\,\mathbf u_i+z\,\mathbf w_i\big) \end{equation}\]第 $i$ 个接触点的合力记为 $\mathbf F_i=\mathbf F_{i,N}+\mathbf F_{i,T}$,并满足 $\mathbf F_{i,T}=\hat\gamma_{i,n}\,\mathbf n_i+\hat\gamma_{i,u}\,\mathbf u_i+\hat\gamma_{i,w}\,\mathbf w_i$, 即 $\mathbf F_i\in\mathcal C_i$。其中 $\mathcal C_i$ 是一枚圆锥:其半角斜率为 $\tan^{-1}\mu_i$,顶点在接触点 $i$,轴线沿 $\mathbf n_i$ 指向外侧。形式化地,
\[\mathcal C_i=\left\{\,\mathbf x=[y,z,t]^{\top}\in\mathbb R^3\ \big|\ y^2+z^2\le \mu_i^2\,t^2,\ t\ge 0\,\right\},\]并以接触点为锥尖、$\mathbf n_i$ 为锥轴方向。
下面展示:从公式(1)推导到公式(2)的过程