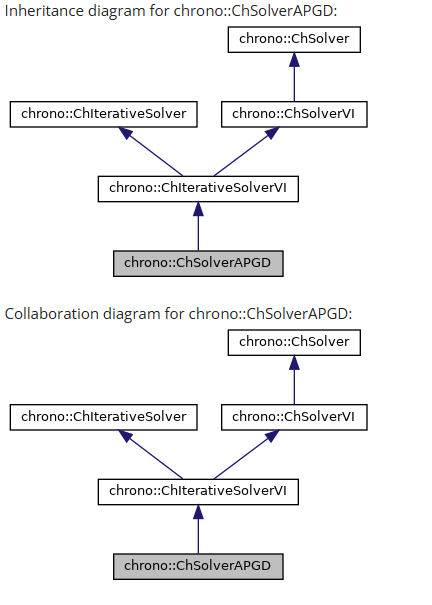
CHRONO 引擎的约束分发与求解机制深入分析

A P G D

APGD求解器官方指导文件

1. CHRONO 中的约束分发机制

CHRONO 引擎采用面向对象的设计，将全局约束矩阵的组装任务分散到各个约束对象中[1]。 每个约束（ChConstraint 派生类）负责提供自己对应的一行雅可比矩阵 [Cq_i]， 全局雅可比矩阵 [Cq] 可以看作由各约束的行按顺序拼接而成[1]。 对于涉及两个物体的约束，CHRONO 提供了 ChConstraintTwo 基类及其派生类。 这类约束同时引用两个 ChVariables 对象（对应两个受约束的物体）， 并维护两个子雅可比矩阵，列数分别等于两个变量向量的维度[2]。 也就是说，每个二元约束有 [Cq_a] 和 [Cq_b] 两个行向量，分别作用于物体A和物体B[2]。 这种机制确保约束力（拉格朗日乘子）对不同物体的作用通过各自的子雅可比矩阵分发，不需要显式构造整个系统的大矩阵。

以碰撞接触为例，CHRONO 用特定的约束类来表示法向约束和摩擦约束。 例如，ChConstraintTwoContactN 表示接触法向的非穿透约束，ChConstraintTwoFrictionT 表示接触面的摩擦切向约束。 对于每一个接触点，CHRONO 会生成一个法向约束和两个正交的切向摩擦约束， 一共三个约束来近似库仑摩擦圆锥[3]（两个切向方向通常称为U方向和V方向，对应摩擦圆锥的基平面）。 法向约束通常被设置为不等式（mode为UNILATERAL），只允许产生非负的法向力， 而摩擦约束被标记为FRICTION类型，可以正负取值[4]。每个此类约束继承自ChConstraintTwo，因此同时包含两个物体的变量和雅可比。 它们在仿真中各司其职：法向约束提供接触正向力，防止相互穿透；两个摩擦约束提供切向摩擦力，抵抗滑动，并共同作用形成摩擦锥。 由于每个约束都持有对应物体的变量引用和雅可比块，它可以直接将约束冲量施加到相关的物体状态上。 例如，ChConstraint 定义了 IncrementState(deltal) 接口，用于根据增量乘子 deltal 更新相关变量的速度/冲量：[5] “v += [invM]*[Cq_i]’ * deltal 或等价地 v += [Eq_i] * deltal”[5] 这里 [Eq_i] 实际上就是预先计算好的 $[invM] \times [Cq_i]’$ 向量。 对于二元约束，IncrementState 会将冲量按 [Eq_a] 加到物体A的速度上， 按 [Eq_b] 加到物体B的速度上，各自权衡了它们的质量矩阵逆$M^{-1}$[5]。 因此，约束力（乘子）的贡献被分发到不同物体的状态增量上，实现了约束作用的局部应用。 概括来说，CHRONO通过这种“每约束一行雅可比、每变量自带质量”的分布式结构， 让多个接触点和约束同时作用时无需组装整体矩阵，每个约束对象自行处理与其相关的变量更新。

2. 变量系统 (ChVariables) 的结构设计

CHRONO 使用 ChVariables 类及其派生类来封装物体的动力学变量（如速度、加速度）及质量信息，以实现分布式的系统表示[6]。 每个 ChVariables 对象对应一个物体或运动单元，包含该单元的自由度数、质量子矩阵（质量和转动惯量等）以及当前的状态向量和力向量等数据。 关键的是，ChVariables 并不一定存储显式的质量矩阵， 而是要求派生类实现与质量矩阵相关的运算接口， 例如计算 $M \mathbf{x}$ 或 $M^{-1} \mathbf{x}$[7][8]。 正如CHRONO文档所述：系统质量矩阵通常不显式组装；在矩阵-自由求解时， 每个 ChVariables 对象通过提供诸如 “将本变量质量矩阵乘以向量” 等操作来参与计算， 从而无需形成全局质量矩阵[6]。 换言之，每个变量对象“知道”如何用自己的质量属性对向量进行运算[9]。 例如：

通过这些接口，迭代求解器可以在需要时按需调用局部质量运算。例如，在计算约束的Schur补值 $g_i = Cq_i M^{-1} Cq_i^T + cfm$ 时， 约束对象会调用相关 ChVariables 的质量逆乘法来得到 $M^{-1}[Cq_i]^T$（即 Eq_i 向量）， 再与 $[Cq_i]` 求点积得到 $g_i$[13][14]。 整个过程中并未显式形成全局质量矩阵或全局雅可比矩阵，而是利用变量对象的接口完成运算。

这种设计保证了系统的稀疏和模块化：每个物体的质量属性（质量标量或质量矩阵块）由其自身管理，求解器只需要调度这些小型运算即可[9]。 此外，ChVariables 还维护了一些元数据，例如变量在全局向量中的偏移量 offset，以及自由度数量 ndof[15]。 在组装全局方程时，系统描述符 (ChSystemDescriptor) 会为每个变量分配在全局状态向量中的位置，并调用 SetOffset 进行记录[16][15]。 这样，当约束或求解器需要访问或修改某个变量对应的全局向量片段时，可以通过该偏移直接定位。 此外，每个 ChVariables 对象通常包含其当前的状态向量（例如速度 $q_b$）和对应的广义力向量 $f_b$，并提供方法访问它们[17]。 这意味着物体的微分状态和受力也由变量对象分散存储和管理。总的来说，CHRONO的变量系统使得整个动力学矩阵呈“块对角”分布存储， 各块由相应物体的 ChVariables 管理，在需要时通过接口参与计算，而不必组装成一个巨大的稠密矩阵[6]。

3. 投影操作 (Project) 的实现方式

为了处理不等式约束和摩擦约束的非线性条件，CHRONO 在 ChConstraint 基类中定义了虚方法 Project()， 用于将当前约束反力（拉格朗日乘子）投影到允许的集合上[18]。默认情况下，Project() 会对单边约束（UNILATERAL）执行非负性投影： 如果乘子 $l_i$ < 0，则强制置零[19][18]。这一默认实现确保诸如接触法向约束不会产生拉力（只允许推力）。 对于双边约束（LOCK模式），默认 Project() 不做任何修改；对于有上下限的约束（例如箱约束）， 则可以在派生类中重载该函数以实现在[min, max]范围内截断乘子[20]。 最复杂的情况是库仑摩擦约束，因为摩擦力的可行域是一个由法向力和切向力共同决定的圆锥体（Coulomb摩擦锥）。 CHRONO 引擎通过特定的约束类和投影逻辑来处理这一情况。 当存在摩擦时，一个接触包含法向约束 ChConstraintTwoContactN 和两个正交切向摩擦约束 ChConstraintTwoFrictionT （或其模板版ChConstraintTwoTuplesFrictionT）[3]。 它们的乘子必须满足耦合条件：法向乘子 $l_n \ge 0$，切向乘子 $(l_{tu}, l_{tv})$ 的范数不超过 $\mu l_n$（$\mu$为摩擦系数）。 CHRONO通过组合投影来实现这一约束：在迭代求解过程中，不独立地裁剪每个乘子，而是将一个接触的法向和两个切向一起投影回摩擦锥集合。 具体而言，ChConstraintTwoContactN（接触法向约束类）重载了 Project() 方法， 以同时修改其自身的乘子 $l_n$ 以及关联的两个摩擦约束的乘子 $l_{tu}, l_{tv}$[21]。 投影算法相当于：首先保证法向力非负，如果计算中出现 $l_n < 0$ 则将其设为0且同时将切向摩擦力清零（意味着接触分离）; 接着检查摩擦圆锥条件，如果 $\sqrt{l_{tu}^2 + l_{tv}^2} > \mu \, l_n$， 则按照摩擦圆锥边界对切向力进行缩放，使其落在圆锥上，即缩放切向分量使 $\sqrt{l_{tu}^2 + l_{tv}^2} = \mu \, l_n$[21]。 这一过程中，三个约束乘子会同时调整，确保满足互补条件 $l_n \ge 0$、$c_n \ge 0$、$l_n c_n = 0$（非黏着时法向力为零）以及摩擦力满足库仑上限。 值得注意的是，在考虑摩擦的情形下，CHRONO并未对法向约束单独执行非负截断， 而是依赖上述锥投影一步完成。[22]指出：“不同于一般的单边约束，这里（有摩擦时的法向约束）并不直接将 $l_n$ 投影为非负， 因为将由‘伴随’的摩擦约束对象对整个锥体进行投影修改所有三个分量。” 换言之，当一个接触包含摩擦时，法向约束的 Project() 不仅管法向力，还会查看和调整两个切向摩擦力，使三者共同落入允许域[22]。 这种设计源自 Anitescu 等人提出的互补求解方法，实现了库仑摩擦锥的精确投影[21]。 通过 Project() 机制，求解器在每次迭代中都能纠正违反约束的不合理乘子值——如负的接触力或超过摩擦锥的摩擦力——从而逐步逼近物理可行解。

4. 在 APGD 求解器中接入类似的投影机制

APGD（加速投影梯度下降）是一种全局迭代算法，也需要在每次迭代中对解向量执行投影，以满足约束条件。为将 CHRONO 的模块化投影机制融入 APGD，可以借鉴其约束分发投影的思想：让每个约束对象自行决定如何投影其对应的乘子分量，而APGD求解器只需统一地调用这些投影操作。具体做法是在APGD迭代的适当阶段（例如梯度步求出暂新的乘子值之后）遍历所有约束，调用每个约束对象的 Project() 方法。由于不同类型的约束已经在各自类中实现了合适的投影策略（例如单边约束截断为非负，摩擦约束投影到锥体），这样做可以将复杂的约束条件处理逻辑隔离在约束类内部，实现求解器逻辑的简洁和通用[18]。 CHRONO 已经采用了类似的设计：ChConstraint 基类的 Project() 提供了默认行为，而各种子类可以根据需要重载此函数，实现各自的投影规则[18]。例如，CHRONO 内部通过派生类实现了“箱式”约束（有上下界时）的投影，和上文提到的摩擦锥投影等[23]。这样，迭代求解器（无论是逐约束的Gauss-Seidel类型，还是全局的APGD）都可以在更新乘子后统一调用 constraint.Project()，而不需要在求解器代码中硬编码各类约束的处理逻辑。这种面向对象的策略模式使得新增约束类型或改变投影策略变得容易：只需实现/修改约束类的投影方法，求解器无需改变。 在实现APGD时，也可以采用类似策略接口或回调机制。如果APGD求解流程难以直接引用约束对象的方法，可考虑维护一个针对约束块的投影函数列表，每个函数知道如何处理特定类型约束的乘子分量。实际上，这与CHRONO当前的做法等效，只是CHRONO通过C++虚函数多态实现了这一分发。采用这种机制，投影的职责从求解器本身转移出来，由约束类或注册的投影函数承担。这样一来，APGD求解器的核心只关注梯度迭代计算，而约束可行域的投影细节（包括摩擦锥耦合判据等)则由独立模块完成。这种设计提高了模块化和可扩展性：当模型中加入新的约束类型（例如黏滞摩擦、限幅铰链等）时，只需提供对应的投影实现并将其接入求解器即可，而不用修改APGD算法的主体代码。 最后，需要注意在APGD中执行投影的时机和方式。由于APGD通常在向量空间进行整体梯度更新，投影应被设计为按接触组独立进行（例如逐个接触或约束对进行），以确保摩擦等耦合条件正确应用。这一点通过CHRONO的设计已体现：一个接触法向约束的 Project() 同时处理其关联的两个摩擦约束（将三者作为一个组投影）[21]。因此，在APGD中可以保持类似思路——按接触/约束组执行投影，以达到模块化和正确性的统一。

5. CHRONO 对接触建模方法的支持范围

CHRONO 主要专注于基于互补约束的刚体接触建模方法，即差分变分不等式(DVI)框架下的补偿接触问题（又称线性互补/锥互补问题）。换言之，CCP（锥互补问题） 是 CHRONO 处理具有库仑摩擦接触的基本方式：法向力和摩擦力满足互补条件和摩擦圆锥约束，通过迭代算法求解[24]。当没有摩擦或忽略摩擦时，接触问题退化为纯粹的LCP（线性互补问题），即只需考虑法向不等式约束（$c\ge0, l\ge0, l \cdot c=0$）。CHRONO 将以上情形统一在它的变分不等式求解器框架中：ChIterativeSolverVI 和其派生类支持双边约束（等式）、LCP约束（不等式，无摩擦）和CCP约束（不等式，含摩擦锥）等不同情况。因此，可以说CHRONO内建的接触模型主要是通过补偿约束来实现无贯穿接触和库仑摩擦的。 在CHRONO的当前实现中，并没有提供独立于互补公式之外的其他接触动力学建模方式（例如基于连续惩罚的渗透模型或光滑NCP函数求解等）。传统的直接LCP求解（如 Lemke 算法等枢轴法）在CHRONO中一般不用于大规模接触求解，因为枢轴法在大量接触时计算代价极高。CHRONO更倾向于使用迭代方法（PSOR、PGS、APGD、ADMM等）近似求解LCP/CCP，以获得较好的可扩展性，允许仿真上万接触的颗粒系统。对于完全线性的约束子问题，CHRONO也支持调用直接线性求解器：例如，当场景中只有双边约束（无不等式约束）时，可组装线性系统并用稀疏LU、QR或者 Pardiso 等直接求解器求解[25][26]。然而，一旦存在非线性的互补约束（如摩擦），就需要迭代投影步骤配合。CHRONO提供的 “PardisoProject” 等求解器类型，实际上仍是在直接线性求解器的框架上结合了投影步骤，以处理互补条件[27][28]——本质上还是变相求解CCP。 关于MLCP（混合线性互补问题）的支持：从概念上讲，CHRONO的接触问题矩阵可以写成典型的KKT形式，即所谓混合互补系统，包括运动学方程和约束方程[29]。CHRONO的框架允许将该系统矩阵装配出来（通过各 ChVariables 的 PasteMassInto 和各 ChConstraint 的 PasteJacobianInto 等接口）[30][31]。对于纯摩擦less接触（LCP），这是一个线性互补系统；对于包含摩擦的接触（CCP），由于摩擦圆锥条件，该系统带有非线性约束，需要迭代求解或线性化处理。如果用户选择，将摩擦锥近似为多面体（即用多条线性约束刻画圆锥），接触问题就可转换为MLCP形式——摩擦力多面体逼近会引入额外的双边或单边约束变量，使问题线性化。但CHRONO并未直接提供这种多面体摩擦选项，而是采用了两个切向约束+锥投影的方法来精确处理圆锥（属于NCP形式的一种处理）。因此，CHRONO求解的大多数接触问题其实属于非线性互补问题(NCP)（因摩擦锥的存在）或其等价的VI表述。它通过迭代方法求解NCP/VI，而不通过牛顿迭代等方法直接求解NCP函数（这在大规模情况下不现实）。 不同接触建模方法对结果精度和收敛性能会有影响。CHRONO采用的DVI（互补约束）法具有不允许侵入的刚性接触模型，能严格满足非贯穿约束，但数值上属于不光滑动力学，会引入速度冲击和震荡，需要较小的时间步长控制稳定性。相比之下，若采用罚模型（并非CHRONO默认），会允许轻微贯穿但模型变得连续光滑，可以用更缓和的积分方法，但需要调节高刚度系数且可能引入震荡。CHRONO的互补法通过调节 cfm（Constraint Force Mixing）参数可以引入一点柔性来改善数值稳定性[32]，相当于给约束增加一点弹性，使问题更接近于MLCP（带对角松弛的线性互补）而易于收敛。不过这也引入了少许允许的约束违反（相当于引入弹性压缩）。在求解器方面，简单的PSOR迭代收敛速度可能较慢，CHRONO提供的APGD等加速算法可明显提高收敛效率，并减少摩擦造成的震荡[33][34]。ADMM求解器则通过将大系统拆分为子问题并交替求解，可能在高度耦合接触（如颗粒堆积）中表现出更好的并行和收敛特性。

综上，CHRONO目前主要支持基于互补约束的接触建模（无论是LCP还是CCP），并配备多种迭代算法来求解这些互补问题。在默认配置下，并没有集成如纯罚式、显式黏滞阻尼接触或光滑NCP函数求解等其他建模途径。如果需要采用其他方法，通常需要在CHRONO框架外自行实现或将接触转化为等效力。目前的互补法已被证明在刚性多体动力学仿真中有效地平衡了物理逼真和计算成本，特别是在大规模接触场景下具有优势。

参考资料：

  1. Tasora, A., & Serban, R. Project Chrono: Chrono::ChConstraint, ChConstraintTwo, ChVariables 类参考和源码[1][2][3][6][21][18]等。上述引用片段来自 CHRONO 8.0/9.0 文档和源代码注释，详述了约束雅可比分块、变量质量矩阵运算、以及投影算法等实现细节。

chrono