总结

同样APGD也不需要使用大矩阵Z；只用过便宜，也就是编号，做乘子计算。

对于ChSystemDescriptor，也就是说，chrono中的建模阶段是通过对不同块的矩阵进行偏移，也就是编码，然后不组装大矩阵Z，看求解器需要不，如果是直接线性求解器，类比VEROSIM中的dantzig，那么我就按照编号把大矩阵组装好，然后进行线性的求解，但是对于APGD这种迭代的求解器暂时不需要大矩阵，那么他在APGD调用相关数据时，比如N和R时，就可以根据偏移编码，读取出数据，从而进行计算，怎么编写的目的是为“既能装配、也能算子式”的通用接口层，方便不同类型求解器插拔。

为什么要matrix-free（矩阵-自由）？

• 避内存 & 避装配成本：大问题（尤其是接触/摩擦）里，显式组装 𝑍的内存会爆；而且每一步接触图都在变，重装配又贵。用算子能省掉海量内存与装配时间
• 适配动态拓扑 ：接触约束的稀疏结构随时间剧烈变化。matrix-free 不依赖固定稀疏图，天然适合“每步都变形”的系统（NSC/碰撞、关节开闭等）。

关于并行化：是在ChSystemMulticore完成的，扁平数组（SoA）+ 并行 kernel（openMP）？这部分之后求解。 matrix-free不绝对是为并行化做准备的。真正把并行吃满的，是 SoA 扁平数组 + 批量 kernel + 颜色/分块避免写冲突（Chrono Multicore 那套）。

算子相对来说更快但是不绝对，主要是出于缓存的考量。

更多的是为了节约缓存

关于ChSystemMulticore是怎么设计完成并行的的，我觉得可以作为后面学习的重点。

关于里面的投影部分，执行约束乘子的投影：将约束的拉格朗日乘子投影到允许的集合上（例如，双边约束不会改变乘子；而对摩擦约束，会把乘子投影到摩擦圆锥上）在CHCONSTRAINT中定义了结构体用来定义Constraint mode，如果时FRICTION选择，ccp投影摩擦锥。

ChConstraintTwoTuplesContactN<Ta,Tb>：法向（Normal, N）约束行

ChConstraintTwoTuplesFrictionT<Ta,Tb>：切向（Tangential, T）约束行（U 与 V 两条）

Simulation system

ChSystem 与两种系统

• ChSystemNSC（Non-Smooth Contacts, DVI/硬接触）：接触约束走互补问题（LCP/VI），可用较大步长、效率高。
• ChSystemSMC（SMooth Contacts, 软接触/罚函数）：接触可变形，常与弹簧-阻尼模型、FEA耦合。

Time steppers（时间积分器）

• EULER_IMPLICIT_LINEARIZED（默认）

  • 一阶、无内迭代、快；支持 DVI(硬接触)；FEA 给一阶精度；约束靠稳定化。

• HHT

  • 隐式、有内迭代、二阶、可调数值阻尼；目前不能用于 DVI 硬接触；适合 FEA/SMC；约束因内迭代收敛“闭合得更严”。

• NEWMARK

  • 与 HHT 类似；除“梯形法则”特参外整体是一阶；多用于 FEA/SMC。

经验：DVI/硬接触 ⇒ EULER_IMPLICIT_LINEARIZED；软接触/FEA/需要二阶与阻尼 ⇒ HHT/NEWMARK。

Solvers（求解器）★重点

时间积分器每步都会调用“求解器”来求未知的加速度与反力。它往往是计算热点。

推荐的迭代求解器与特性：

• PSOR

  • 最常见入门选择；实现简单、收敛精度偏低，质量比奇怪时易卡；
  • 支持 DVI/硬接触；
  • 适合小规模、精度要求不高的场景。

• APGD（加速投影梯度）

  • 收敛好，高精度仿真常用；支持 DVI/硬接触；
  • 对大问题更稳健，建议优先于 PSOR。

• BARZILAIBORWEIN（BB） （后期是否考虑？）

  • 收敛也不错；支持 DVI/硬接触；
  • 与 APGD 相近，有时在大质量比下更鲁棒。

• MINRES

  • 适合 FEA；当前不支持 DVI/硬接触；
  • 配合对称稀疏线性系统，常与预条件配合使用。

• ADMM + PardisoMKL

  • 同时支持 FEA 与 DVI；
  • 需要内部线性解算器，最佳是 PardisoMKL（需单独模块），否则退化到 ChSolverSparseQR。

chrono 求解器结构

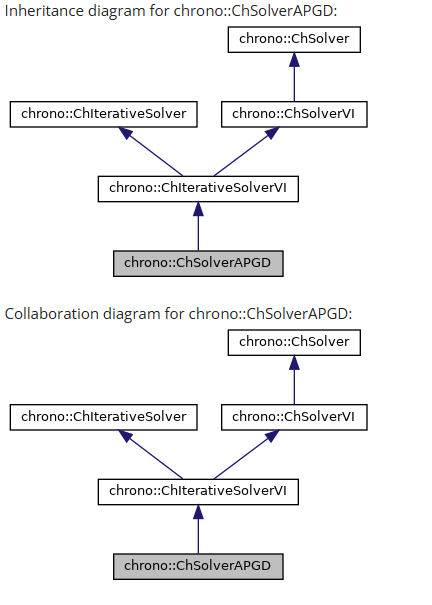
代码

ChVersion : 版本号头文件”（version header）

Chplatform: Chrono 的“跨平台胶水” ，ChApiEXPORT/IMPORT 解决不同平台/构建方式下动态库符号可见性问题；CH_DEPRECATED 用于标记弃用 API并在编译期发出友好提醒。

ChApiCE: ChApi 是一个“可见性贴纸”宏——你把它贴在要对外公开的类/函数前面，它会在编库时展开成“导出符号”，在用库时展开成“导入符号”；如果是静态库或非 Windows，它通常什么也不做。

ChClassFactory:工厂机制

ChSystemDescriptor:

• CH_FACTORY_REGISTER(ChSystemDescriptor):注册进 Chrono 的类工厂（ClassFactory）这个类能被按名字动态创建/持久化；

• CH_SPINLOCK_HASHSIZE:并发用的自旋锁分片大小;

• ChSystemDescriptor() and ~ChSystemDescriptor():构造/析构把计数/参数复位、容器清空，但不负责删除外部对象。

• ComputeFeasabilityViolation: 扫一遍所有约束，统计“最坏的违反量”和“（单边）互补残差的最坏值”，用于判断这一仿真步的约束是否“解干净了”。

• CountActiveVariables and CountActiveConstraints:“统计 + 编号（写偏移）”的工具，用来把当前步中激活的变量/约束映射到全局向量里的正确位置。

• UpdateCountsAndOffsets : 一次性刷新“计数 + 偏移”并开启缓存。

• PasteMassKRMMatrixInto：把变量侧的大块 𝐻（质量/刚度/阻尼的组合）贴到全局稀疏矩阵 Z 的指定位置。 如图所示：。

• PasteConstraintsJacobianMatrixInto and PasteConstraintsJacobianMatrixTransposedInto: 把雅可比和雅可比转置贴到全局稀疏矩阵。

• PasteComplianceMatrixInto ： 约束顺应矩阵（compliance matrix）E贴到一个稀疏大矩阵 Z 的指定位置。

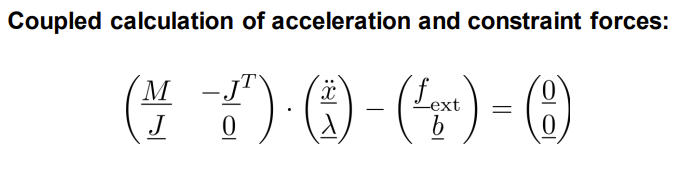
• BuildSystemMatrix:一次线性化方程组装成“整块稀疏矩阵 Z 和右端向量 rhs”

• BuildFbVector: 按活跃变量（刚体/节点等）的全局偏移，把每个变量贡献的“已知力”写入系统级向量 𝑓

• BuildBiVector:按活跃约束的全局偏移，把每条约束的右端项写入系统级向量 𝑏

• BuildDiVector(Dvector) :一次性得到系统 RHS 的拼接向量 𝑑={𝑓;−𝑏}（注意下半部分有负号），直接与 𝑍∗𝑦−𝑑 的实现对接。

• BuildDiagonalVector:构造系统矩阵 𝑍 的“对角近似”向量，用于对角预条件或尺度化。

• FromVariablesToVector： 从所有“活跃”变量中把它们当前的未知量状态收集起来，拼成系统级变量向量 𝑞，写进 mvector。

• FromVectorToVariables： 把外部给出的系统级变量向量（长度应等于活跃自由度总数）散回每个变量对象的 State()。

• FromConstraintsToVector and FromVectorToConstraints:对“约束乘子向量 𝑙”做收集/回填（gather/scatter）的两段工具函数,和上面写的一样。

• FromUnknownsToVector and FromVectorToUnknowns: 整根未知量向量 ，q 和 l; 操作同上。

• SchurComplementProduct：Schur 补矩阵的矩阵-向量乘， 完全matrix-free， 不显式组装 N。

• SystemProduct： 按块结构“算子式”地计算整块KKT矩阵 𝑍与向量 𝑥的乘积。

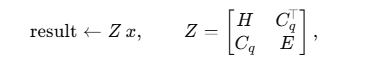
• ConstraintsProject： 把“乘子向量”投影回可行集合。
• UnknownsProject ： 同上
• WriteMatrixBlocks：把系统矩阵的各个“基本砖块”与 RHS 分别导出到磁盘。
• WriteMatrix： 显式装配法——直接调用装配函数得到稀疏矩阵 𝑍 和右端 rhs，写盘。
• WriteMatrixSpmv：算子（SPMV）重建法——不给出 𝑍，而是对每个标准基向量 𝑒𝑖 计算一次。

总结一下chrono的建模逻辑：

如果问的是“在建模阶段（BeginInsertion→EndInsertion）到底有没有把整块大矩阵 Z 真正组装出来？”

——答案是：没有。

在建模阶段只是把对象化的稀疏数据（变量、约束、K/R/M 块）登记到 ChSystemDescriptor 里，并给它们编号/写偏移。此时系统里保存的是：

• 每个变量块自己的 $M$、$M^{-1}$、已知项 Force()；
• 每条约束自己的一行雅可比 $J_i$、右端 $b_i$、以及可选的对角 CFM（顺应）项 $E_{ii}$；

• 可选的 ChKRMBlock 子块矩阵（刚度/阻尼等）。 这些都只是分散的小块/对象，不是整块 $Z$。偏移是在 EndInsertion() 后统一计算好的。

  K/R/M 块就是把变量侧“惯性-阻尼-刚度”这三件事打包成一类通用稀疏子块。 E 就是约束的“顺应/正则化矩阵”（compliance，也叫 CFM = Constraint Force Mixing）。

什么时候才“真的组装大矩阵 Z”？

只有在你明确调用组装相关接口或用直接线性求解器时，才会把整块

显式贴到一个稀疏矩阵里。对应接口是 BuildSystemMatrix(&Z,&rhs)，内部顺序就是： PasteMassKRMMatrixInto(H) → PasteConstraintsJacobianMatrixInto(J) → PasteConstraintsJacobianMatrixTransposedInto(J^T) → PasteComplianceMatrixInto(E)，然后 BuildDiVector(rhs) 生成 ${f;-b}$。

• 你在 WriteMatrix(...) 里也能看到，它就是先调 BuildSystemMatrix 再写盘的：这说明显式装配是在需要时才做。
• 另外还有 WriteMatrixBlocks(...)，是把 $H,J,E,f,b$ 分块导出（也不是整块 $Z$）。

迭代求解时并不需要显式 Z

• MINRES / 其它 Krylov：用 SystemProduct(result, x) 做算子式乘法（SPMV）来代替显式 $Z$ 乘法；这就是“矩阵-向量乘不组装矩阵”的做法。WriteMatrixSpmv(...) 甚至用“对每个单位向量做一次 SystemProduct”按列重建 $Z$ 来做调试对比。
• PSOR / VI/CCP（乘子空间）：用 SchurComplementProduct(result, l) 直接算 $Nl=(J\,M^{-1}J^{\top}+E)l$，也不需要显式组装 $N$。

ChSolverAPGD：