WEEK 14（11.08.2025-15.08.2025）

1.LCP → QP (多体系统LCP模型转换为QP的严格性分析)
继续步长问题
对比一些chrono看看是不是少东西（漏了某些特性）

2025.08.11

Task: LCP -> QP

关于LCP和QP问题的转化是否是近似的？

详细回答了这个问题。

2025.08.12

Task: 步长问题

在探讨步长问题时，我在思考 外部时间步 ℎ（物理/积分层）来自RBDClusterLagrangeMultipliers 及上层，和APGD求解器中的步长更新是否是一个值，内部是指的迭代步长。

我现在去重新理解伪代码，从而来解决这个问题：

两个“步长”其实是两个不同层面的概念，一个是外部仿真时间步长，一个是APGD 算法内部的迭代步长

外部时间步长（simulation time step, Δt）

由你的物理系统或仿真主循环控制，比如 RBDClusterLagrangeMultipliers 上层代码设置的 h = 0.001 s。
这个 Δt 决定了 一次物理积分要前进多少真实时间。
在每一个 Δt 内，求解器（APGD、Dantzig 等）会被调用一次，用来解这一步的约束方程。
它不会随着 APGD 的迭代改变，是固定的外部参数。

内部迭代步长（APGD 的梯度步长，t 或 tk）

是 APGD 算法内部用来更新解向量 $\lambda$ 的“学习率”。
计算方式通常是：
\[t_k = \frac{1}{L_k}\]
其中 $L_k$ 是 Lipschitz 常数的估计值（梯度变化的“斜率”上界）。
在你的实现里，可能会有：
```
Lk = 0.9 * L_temp;
tk = 1.0 / Lk;
```
这个 tk 是 每一次迭代用来控制更新幅度的参数。
它是数值优化里的步长（step size in optimization），与外部 Δt 没有直接耦合，但 Δt 越大，梯度值会变大，可能间接影响到 Lk 的估计。

它们的关系

外部 Δt 决定物理系统积分的稳定性和精度。
内部 tk 决定 APGD 每次迭代更新的快慢。
外部 Δt 变大 → 系统矩阵 Z、右端项 b 会变化 → 梯度的 Lipschitz 常数 Lk 可能变大 → 内部 tk 变小。
两个步长不直接等价，但是外部 Δt 会通过物理方程影响到内部 tk 的取值范围。

📌 直观类比

外部 Δt：你开车时每秒看一次地图（仿真采样频率）。
内部 tk：你每次修正方向盘的力度（算法迭代更新幅度）。
看得太慢（Δt 太大）会让方向修正困难，需要更小的转向幅度（tk 更小）才能不翻车。

这段迭代的目的，就是在一次物理时间步内，通过多轮更新和步长调整，让 APGD 收敛到一个稳定、可行、下降充分的解，确保数值稳定性和收敛速度。

关于步长问题总结

外部也就是我们在UI界面设置，RBDscene中传进来的外部时间步长，是固定的，而内部时间步长和这个完全不一样。

外部时间步长：仿真每一步推进的物理时间长度。
内部时间步长：在同一 Δt 内不断调整 λ，用步长 tk 控制每次走多远，直到找到收敛解。

也就是每个外部的时间步长，我都需要从头去计算一次最优解，而内部时间步长的意义是为了不断调节每步的大小，更快，更准的找到最优解。

2025.08.13

task:测试chrono demo 用来验证步长是否发生了变化

实验详解：

Chrono 小实验总结：APGD 求解器在接触场景中的表现

实验目的

验证在 Chrono 框架中使用 APGD（Accelerated Projected Gradient Descent） 作为接触求解器的运行情况。
理解外部时间步长（time_step）与 APGD 内部数学步长（t_k）的区别。
检查 L_k（Lipschitz 常数）和 t_k 在实际仿真中的变化规律。

场景搭建

使用 NSC（Non-Smooth Contact） 接触模型。
切换求解器为 ChSolver::Type::APGD，最大迭代次数设为 100。
场景元素：
- 圆柱体：质量 1500 kg，半径 0.5 m，高度 0.8 m，从高度 2.65 m 自由下落。
- 地面：固定刚体，尺寸 2×1×2 m。
碰撞系统：MULTICORE + HYBRID 窄相算法。
可视化：Irrlicht 渲染，实时显示接触力。

关键观测

接触未发生时

sys->GetNumContacts() = 0
APGD 内部 nc = CountActiveConstraints() 为 0
初始化 Lk 时：
\[L = \frac{\| N (\gamma - \hat{\gamma}) \|}{\|\gamma - \hat{\gamma}\|}\]
因分母为 0 → Lk = inf，t_k = 0
打印结果恒为：
```
Lk = inf   tk = 0
```

接触发生后

nc > 0 时，才会计算出有效的 Lk 和 tk。
如果打印逻辑没有加 nc 检查，就会在无约束时也输出无效值。

外部步长 vs 内部步长

外部时间步长：time_step = 1e-3 s（积分推进量）。
内部步长：APGD 的 t_k，由 1/Lk 决定，是数学迭代参数，与物理时间步长无关。

最终效果图：

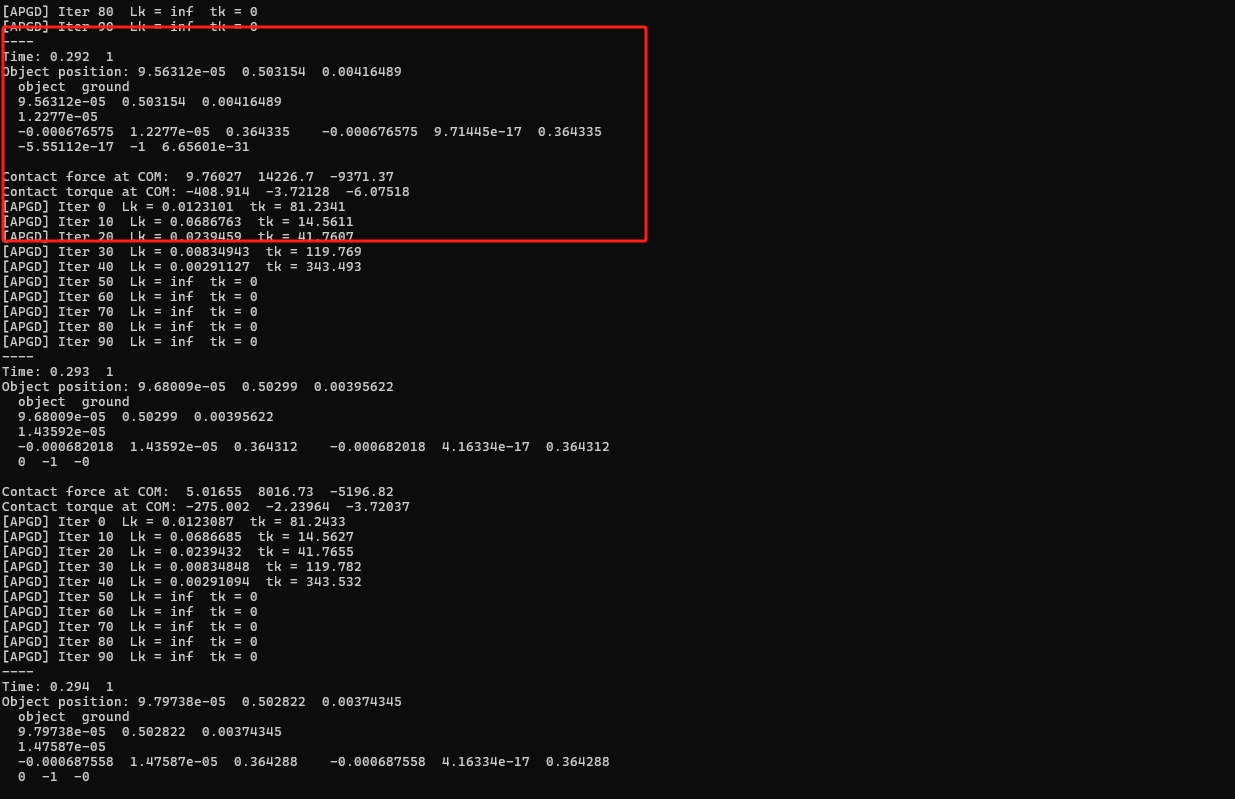
Apgd Dt T Test

2025.08.14

task: chrono src

2025.08.15

task:右端项 𝑟（即 Chrono 的 𝑏schur）的构造

改了一天，改崩了，现在还原版本，周一在继续尝试。